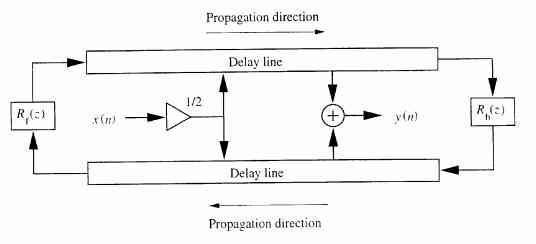
2つのディレイラインはダランベール方程式の解を離散化したものと解釈できる。進行波と反射波の波形はディレイを通り、反射フィルタで位相逆転と周波数に依存したダンピングを受けながら反射する。入力は、両ディレイのある場所に加算され、同時に、観測点から両ディレイの値を取り加算し、出力される。
モデルの仮定として、サンプリング定理を満足するよう信号が帯域制限されていることが必要である。線形時不変システムという仮定から、弦の損失や散乱は、弦上の任意の駆動点、観測点間で交換可能である(Smith 1992,1997)ので、実現の容易な無損失ディレイラインが使用可能となる このモデルの入出力は、変位、速度、加速度、傾斜(Morse 1976,Smith 1992)など何でもよい。加速度を波形の変数に取ると、理想的な弦の弾き入力は単位インパルスになる。このようにシンプルな系を考えると、終端、拡散、損失などの要素を、Fig2のようなシングルディレイに置き換えることができる。
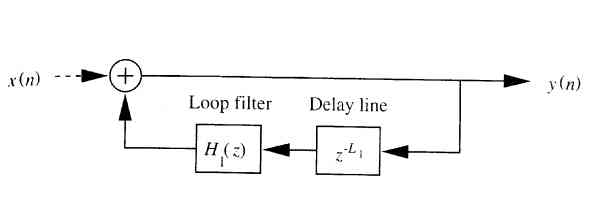
<Fig2>単純化した線形弦モデル「シングルディレイライン(SDL)モデル」
Karplus-Strongアルゴリズムは、本モデルの、励振入力を
ディレイラインの初期値とした場合に相当する
極端な場合、損失や散乱を、弦を伝播する1周の経路の1個所にまとめることができる。ここで、ループフィルタを、y(n)= (x(n)+x(n-1))/2とし、弦の初期条件として乱数をセットすると、Karplus-Strongのアルゴリズムと同じになる。この場合はシステムに明示的な入力信号がないことに注意。
【双方向ディジタルウェーブガイドからSDLモデルへ】
Fig2のモデルが、基本のみに極端にシンプル化した合成モデルであるが、合成音の質向上と物理モデルの理論的理解のため、もう少し詳細なモデルを作る必要がある。ここでは、双方向ウェーブガイドモデルとSDLモデルの関係を詳細に調べていく。
双方向ウェーブガイドモデルとSDLモデルの2つの基本型の関係について考える。
(1) ブリッジ出力を持つもの、
(2) ピックアップ出力を持つもの
を考える。
実際の物理的な弦を撥弦により励振したとき、互いに逆方向に独立に伝播する2つの波が生成される。出力(例えばアコースティック楽器のブリッジに働く力とか、エレクトリックギターのピックアップの出力電圧)は、これら2つの波の反作用として励起される。励振の効果やピックアップ位置などは、Fig1のように2つのディレイを持つウェーブガイドモデルで容易にシミュレーションすることができる。しかし、合成のためにはFig2のようなSDLモデルの方が効率的である。したがって、理論的な立場から、「励振の効果やピックアップ位置を含んだSDLモデル」を定式化することは興味深いことである。理想的な速度、加速度入力で励振される弦のモデル(それぞれ、弦を弾くことと叩くことに対応する)は、単位インパルスで近似できることが示されている(Smith1972)。
そこで、線形時不変を仮定して、この系をインパルス入力を持つ線形フィルタとして考えていくことができる。
■ブリッジ出力を持つ撥弦
以下の議論で、このモデルの伝達関数をラプラス変換で表す。(ここではラプラス変数sをjωと書く)。その後、これをZ変換の形に近似する(Oppenheim他参照。ラプラス変換の詳細は省略)。
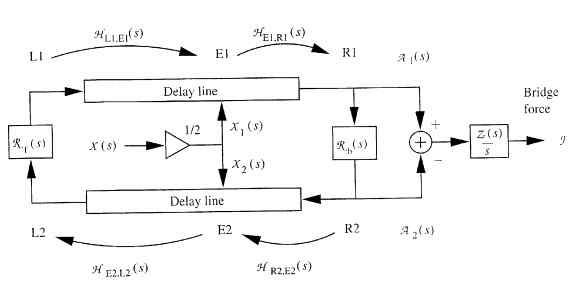
Fig3で、理想的に撥弦されたデュアルデェレイのウェーブガイドモデルを、横断するブリッジを出力として持つモデルに変換する。このような状況は、アコースティックギターに当てはまる。ここで、HA,B(s)は、AからBへの伝達関数を表す。入力は x1(s)=x2(x)=x(s)/2のように半分づつ2つのディレイラインに分ける。
まず、単純なモデルとして、E1とE2の二点から励振するのと等価な効果を生むように、E1一点から励振する方法を考える。ブリッジの終端R1、R2がFig1のように入力点E1,E2の右にあると仮定すると、このような2点励振と等価な一点励振入力は式(1)のようになる。
ここで、"eq"は等価を意味し、XE2,E1(s)は、E2からE1への左側伝達関数(これはE2からL2、L1からE1への部分伝達関数と、反射係数Rf(s)を含んだもの)を意味する。(注:E2から入力されたx2(s)を、E2→L2→L1→E1と回ってきたものがE1から入力されたものだと考える)。したがって、HE(s)は等価励振伝達関数である。
ここで、欲しい出力信号はブリッジでの横断力F(s)である。これは計算すると、
F(s)=F+(s)+F-(s)=Z(s)[V+(s)-V-(s)]=Z(s)[A1(s)-A2(s)]/s (2)
となる。この式は、+、-記号は伝播方向を表す。この式は、ブリッジに働く力はブリッジインピーダンスZ(s)と、ブリッジでの弦の速度V+(s)とV-(s)の差を掛けたもの、ということを表す。ここで、加速度の差A1(s)-A2(s)は、演算子1/sで積分され、速度差V+(s)-V-(s)に変換する。そうすると、
F(s)=Z(s)[A1(s)-A2(s)]/s
=Z(s)[A1(s)-Rb(s)A1(s)]/s (3)
=Z(s)[1-Rb(s)]A1(s)/s
=Hb(s)A1(s)
ここで、Hb(s)はブリッジの加速度→力伝達関数である。したがって、
A1(s)=HE1,R1(s)XE1,eq(s)+Hloop(s)A1(s) (4)
ここで、Hloop(s)=Rb(s)・HR2,E2(s)・HE2,E1(s)・HE1,R1(s) (5)
すなわち、Hloop(s)は、このシステム全体を信号が一巡する伝達関数である。
したがって、式(4)の各項はそれぞれ、等価励起信号XE1,eq(s)がR1に伝わる伝達関数と、信号A1(s)がループを一巡することに対応している。これより、A1(s)は次のように計算できる。
A1(s)=HE1,R1(s)・1/(1-Hloop(s))・XE1,eq(s)
=HE1,R1(s)S(s)XE1,eq(s) (6)
ここで、S(s)は弦のループの再帰効果による弦の伝達関数と考えることができる。これら全てをまとめ、励振からブリッジまでの伝達関数を求めると、
HE,B(s)=F(s)/X(s)=1/2・[1+HE2,R1(s)]・HE1,R1(s)/(1-HLoop(s))・
Z(s)・1/s・[1-Rb(s)] (7)
あるいは、さらに簡略化すると、
HE, B(s)=HE(s)・HE1,R1(s)S(s)HB(s) (8)
と書ける。これは弦の各システムが直列接続されている形になっている。
ここで、ラプラス変換の形で記述したギターのモデルを、離散時間モデルのz変換の形に近似する。この近似は、離散時間でモデルを動作させるために必要である。
(8)式をz変換の形に変形する。
HE, B(Z)=HE(Z)・HE1,R1(Z)S(Z)HB(Z) (9a)
ここで、
HE(Z) = 1/2・[1+HE2,E1(Z)] (9b)
S(Z)=1/[1ーHloop(Z)] (9c)
HB(Z)=Z(Z)I(Z)[1-Rb(Z)] (9d)
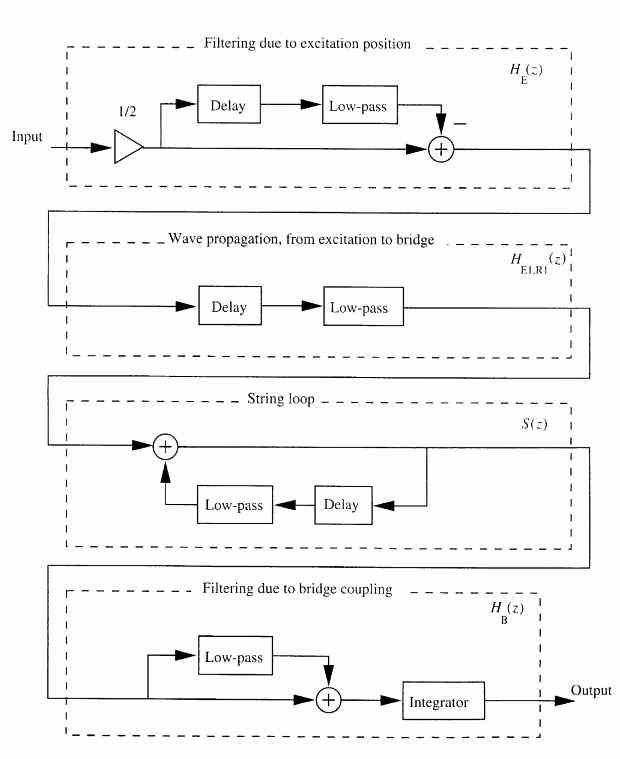
ここで、フィルタI(Z)は、時間積分を離散時間で近似したものである。式(9a)の結果をFig4のようなブロックダイアグラムと解釈する。
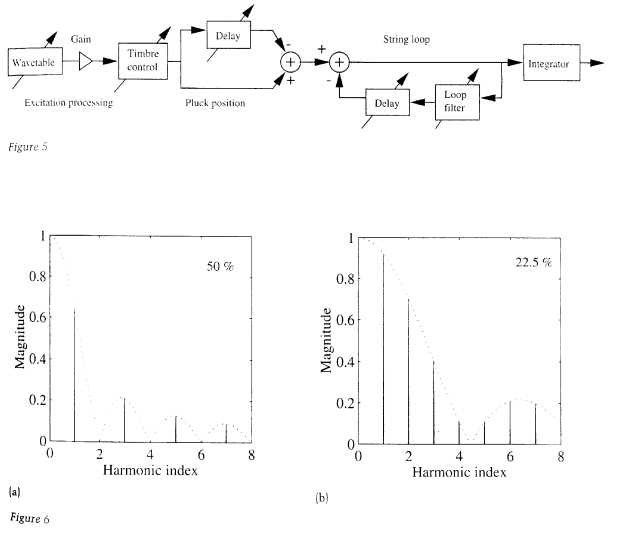
弦ループのディレイ(の遅延量)は連続可変できる必要があり、
微小ディレイフィルタで実現できる
ブリッジから撥弦位置までの弦の全長に対する相対距離を50%にした場合(a)、22.5%にした場合(b)
これは式9を、質的に遅延やフィルタの離散システムの伝達関数で近似したものである。
ここで、Fig4の一番上のブロックに、反射伝達関数HE2,E1(Z)のマイナス符号があることに注意。一方で、一番下のブロックは、RB(Z)のマイナス符号は式9(d)のマイナス符号にキャンセルされる。
実際の音合成のためには、Fig5に示したような単純化したモデルで、音の劣化無しに近似することができる。以下、Fig5を元に単純化を示す。式9(b)の伝達関数HE2,E1(Z)はほとんど無損失ディレイと等価で、励振点のローパスフィルタは省略することができる(あるいは、1よりほんの少し小さい定数でおきかえることができる)。次いで、普通の演奏状態では、励振点E1からブリッジ点R11までの伝播もまたほとんど無損失ディレイと等価であるので、これを省略しても影響は知覚できない。式9cの弦ループS(Z)は、ディレイとローパスフィルタは音質に大きな影響があるので省略することはできない。最後に、式9dで表される、ブリッジ部分 HB(Z)の[1ーRb(Z)]であるが、これは定数2と近似することができる(Rb(ejω)≒−1である)。以上で省略した部分の誤差は、Fig5の、音色コントロールフィルタで補正することができる。
Fig5の合成モデルはいくつかの調整可能な要素を含んでいる。励振テーブルは有用な波形、たとえば単位インパルスや、「複雑に加算された励振波形(complex aggregate excitation)」(Smith1993,Karjalainen,Valimaki,Janosy 1993)などが考えられる。たとえば、楽器の胴体の共鳴の効果は、線形時不変の仮定により、励振にまとめてしまうことが可能なので、ここで実現するのが効率的である。また、このテーブルのデータを補間して励振信号を生成することも可能である。ゲインコントロールは単なる乗算器である。音色フィルタは、高音の強調または減衰を行い、鋭利なアタックやソフトなアタックを実現するための、1〜2次の再帰型フィルタである(Jaffe and Smith 1983)。音色制御フィルタは、(音程が変わっても)音のアタックの印象が変わらないようにするために、基本周波数に合わせて音色制御フィルタの特性を変える必要がある。撥弦位置コントロールは、可変型の櫛形フィルタで、ディレイの遅延時間は、Fig3で励振信号がE2→E1の左回りの経路で伝わる時間に合わせる。実際には、これはE1→E2の右回りの経路の遅延時間で代用することもできる(一般にはこちらの方が短い)。こうしても、アタックの変化はほんのわずかだからである。櫛形フィルタは、周波数がfm=m/td(tdは櫛形フィルタの遅延時間(秒)、mは整数)であるような複数のゼロ点を作る。 ブリッジ出力積分器は、カットオフ周波数が、発生する最も低い基本周波数よりも低いような1次のIIRローパスフィルタで近似できる。撥弦位置コントロールと出力積分器はいっしょに考えることができる。周波数0のとき、前者のゼロ点は後者の極で打ち消されるからである。Fig6に、両フィルタを1つの伝達関数にまとめた場合の効果を示す。撥弦位置は、弦の長さに対する撥弦位置からブリッジまでの距離の相対値という形で現れている。たとえば、50%とは、弦の中央を意味する(Fig6a)。この効果は、従来の撥弦の振る舞いの解釈(Fletcher Rossing 1991,Figure2.5[Page 39],Figure 2.7[Page 41])と等価である。
Fig5の弦ループはFig2のものと同じものである。遅延器ブロックは、あらゆる音程を発生するために、遅延時間の微調整ができる必要がある(Jaffe,Smith 1983).これは、1次のオールパスフィルタやラグランジェ補間などを用いた、端数遅延フィルタ技術(Fractional Delay Technique)によって実現できる(Laakso,Valimaki,Karjalainen,Laine 1996).また、ループフィルタは、高調波成分の減衰を弦の長さやその他の弦のパラメータに対応させるよう制御できる必要がある。一般的な方法はゲインとカットオフ周波数の2つのパラメータを持つ1ポールのディジタルループフィルタである(Jaffe,Smith 1983,Valimaki他 1996)。
■ピックアップ出力を持つ撥弦
次に、エレクトリックギター等、磁気ピックアップのような速度検出型センサで出力を取り出す撥弦楽器の伝達関数と合成系のブロックダイアグラムを導出する。Fig7にこの場合のデュアルディレイラインウェーブガイドモデルを示す。ピックアップ位置はO1、O2で示した。
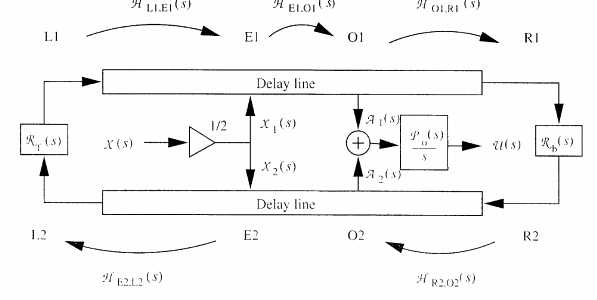
Fig3とFig7を比べると、両者の励振伝達関数は同じであることがわかる。したがって、式4はピックアップ出力の撥弦でも適用でき、その場合はピックアップ位置O1、O2が励振位置はE1、E2の右側にある必要がある。
出力信号は、磁気ピックアップの電圧のような変数で、ピックアップ位置での弦を横切る速度(右行きと左行きの成分の和)に比例する。速度ν(s)は加速度の時間積分に比例し、ピックアップの電圧出力υ(s)は次式のように書ける。
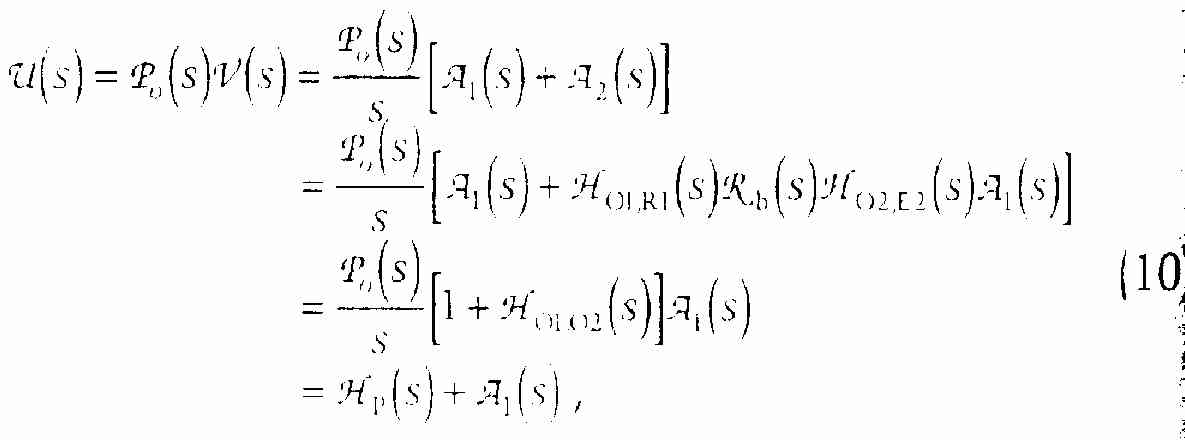
ここで、ピックアップの伝達関数p0(s)はギターのピックアップマイクロフォンをモデル化している。磁気ピックアップでは、p0(s)は通常2次のローパスフィルタになる。Fig7の出力の積分器1/sもこのモデルに含んでいるので注意のこと。
式4に対応して、次のように書くことができる。
A1(s)=HE1,O1(s)XE1,eq(s)+Hloop(s)A1(s) (11)
整理すると、
A1(s)=HE1,O1(s)・1/(1-Hloop(s))XE1,eq(s)
= HE1,O1(s)S(s)XE1,eq(s) (12)
式(1)、(10)、(12)から、励振からピックアップまでの全体の伝達関数を導くことができる。
HE,P(s)=U(s)/x(s)=1/2・[1-HE2,E1(s)]・HE1,O1(s)/[1-Hloop(s)]
・Po(s)/s・[1+HO1,O2(s)] (13)
または、前述の表記を使ってより簡潔に整理すると、
HE,P(s)=HE(s)HE1,O1(s)S(s)HP(s) (14)
ここで、ピックアップ点が励振点E1より左側にあるとすると、この式の添え字の1、2を交換(弦の終端L、Rの交換に相当)した、同様な式が得られる。
ブリッジ出力の場合と同様に、ラプラス変換の形で表現された連続時間システムから、Z変換の形で表現された離散時間の形に近似を行う。
HE,P(Z)=HE(Z)HE1,O1(Z)S(Z)Hp(Z) (15)
ブリッジ出力モデル(式7)とピックアップ出力(式13)の違いは、次の2点である。まず第一に、励振点から出力までの並みの伝播特性,HE1,R1(s)とHE1,O1(s)では、波が伝播する弦の長さが異なる。通常の演奏条件では、弦の波の伝播はきわめて損失が小さいため、この距離の違いは無視できる。第2に、伝達関数は出力のカップリング形態に依存するが、両者の伝達関数は非常に異なる。ブリッジRでの加速度の違いが相対的にフラットな応答であるとき(式3とFig3)、この2つの加速度波のピックアップ位置Oでの和によって、励振点でのフィルタ効果と同様、櫛形フィルタ効果が生み出される(式10、Fig7)。したがって、弦速度を検出するピックアップを持つ弦楽器のモデルは、Fig4のように単一ではなく、2つの櫛形フィルタの直列接続によって音が色付けされる。ピックアップの弦出力段のブロック図をFig8に示す。
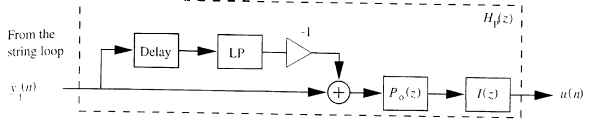
ここでも、弦の端の反射によるマイナス符号は明示的に−1と表される(Fig4参照)。
ピックアップ出力を持つ撥弦による音合成モデルも、ピックアップ点櫛形フィルタとピックアップフィルタP0(s)を直列接続する必要がある点以外は、Fig5と同じになるであろう。この櫛形フィルタはFig5の撥弦位置フィルタと同様のもので、ピックアップフィルタは2次のローパスフィルタが使用できる。
以上で導いた合成モデルは、励振集約技術(Commuted aggregate excitation technique,Smith 1993,Karjalainen,Valimaki,Janosy 1993)を用いてさらに単純化することができる。これは、その他の部分(たとえば楽器の胴体等)のインパルス応答(の効果)を、励振波形に畳み込んでおき、それを(励振波形の)ウェーブテーブルに記憶しておけばよい。もし、弦ループとは別のすべてのコンポーネントをまとめることができれば、明示的な入力を持つKSアルゴリズムの変形というアプローチをとることができたことになる。いろいろな変形が考えられる。弦ループをも励振波形にまとめてしまうもの(これは純粋なウェーブテーブル合成である)から、FIG5のようなSDLモデル、あるいは、Fig3のような完全な双方向ウェーブガイドモデルとしてもよい。このことは、物理モデリングが、ソースフィルタモデリングやサンプリングなどの伝統的な合成技術と互換性があることを示している。シンプルなモデルにするほど計算効率が向上するが、その分、フレキシビリティやパラメータによる制御性が犠牲となる。
【SDLモデルの更なる拡張】
以上で導いたSDLモデルは撥弦楽器の物理モデル合成系を開発する場合に有用な拡張性の優れたビルディングブロックである。SDLモデルは双方向ディジタルウェーブガイドに比べて効率がよいが、それは基本的な信号処理ブロックが最大限に整理され単純化されているからである。たとえば、ピッチを微調整するための、微少時間遅延フィルタなどのブロックは十分に洗練されている。しかしながら、弦の挙動は本質的に非線型であったり、時変系であったりするので、双方向ウェーブガイドというスタイルが必要である(たとえばKarjalainen,Backman,Polkki 1993). SDLモデルにより細かな部分を補足して、音の自然さやその他の音質を改善することが可能である。Fig9に、要素を追加した拡張モデルを示す(Valimaki他 1996).

弦のモデルの励振部は、撥弦励振と胴体の共鳴の要素を含むウェーブテーブルで実現した。こうすることで実現が容易になり効率が非常に向上した(その代わり物理モデルとは言えない)モデルとなっている(Smith 1993,Karjalainenn,Valimaki,Janosy 1993).
撥弦方法や音質が異なる場合のウェーブテーブルを用意して切り替え可能にしてもよい。撥弦シェイピングフィルタE(z)は、ある撥弦テーブルの音色を微調整するのに使用できる。櫛形ノッチフィルタは撥弦位置とピックアップ位置の効果を容易に付加することができる。撥弦位置フィルタP(z)はFig9に示したがピックアップ位置フィルタは描いていない。
弦の振動の2つの偏向によって生じる(天板の縦と横の振動)うなりの効果は2つの弦モデルの出力の合成で実現できる(Jaffe,Smith1983)。2つのモデルのピッチがわずかにずれていると、自然なうなりの効果が生じ、「シンセサイザーのような音」という不自然な感じをぬぐうことが出来る。2つの偏向モデルでのパラメータずらしの効果の例をFig10に示す。
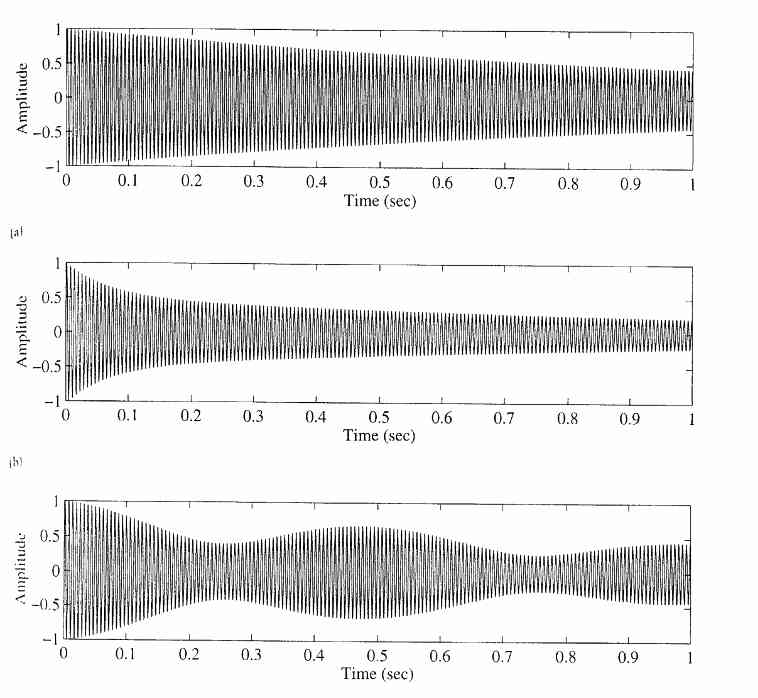
Fig10aでは2つのモデルのパラメータは同じで、指数関数的に出力が減少している。Fig10bは両モデルの基本周波数は同じで、ループフィルタのパラメータを変えたところ、出力は2段階で減衰した。Fig10cではループフィルタのパラメータは等しく、周波数を ずらしたところ、うなりが生じた。
複数の弦の間の相互作用的結合をシミュレートする理論がいくつか提案されている(Jaffe,Smith 1983,Smith 1993,Valimaki他1996).
物理的に修正する方法〜ブリッジ結合フィルタを用いたもの〜を、Smith(1993)が提案している。Fig9のモデルに単純なフィードバック結合を追加し、弦の間の相互作用をシミュレートする。このアプローチは潜在的に不安定である。それは、全ての弦の出力が、すべての弦の入力にフィードバックしているからである。出力信号間のフィードバックに、小さなゲイン係数をかけて減衰すれば、安定にシミュレーションすることができる。それでも、本質的に安定な干渉結合モデルを使った方が安全である。JaffeとSmith(1983)は、撥弦されたメイン弦と、それとは独立して、メイン弦の出力から影響を受ける結合バン クを提案した。この方法は常に安定である。しかしながら、独立して影響を受ける弦のモデルより、楽器モデルの励振された弦自体が他から影響を受け振動するモデルの方がより理想的である。次の章で、このようなモデルの導出を行う。
【結合現象】
Fig11に、2つの偏向を持つ撥弦モデルを修正したものを示す。
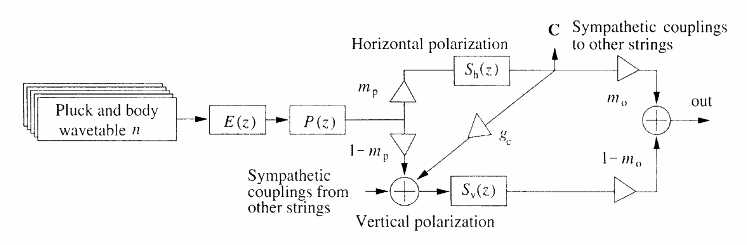
ここで、結合振動の入力は、2つの偏向弦の一方から得る(Fig11えは水平偏向弦の出力を用いている)。フィードバックを避けるために、他の弦からの入力は結合出力を持たない弦にのみ加算する。これは、結合入力は縦偏向弦のみに行うことを意味する。すなわち、出力は横偏向弦のみから出力するからである。このような信号結合は本質的に安定であり、リアルな結合現象を実現することができる。さらに、独立した結合弦を使う必要がない。そうしなくとも合成モデルの全ての弦による結合振動が自然に得られるからである。
このアルゴリズムを一般化する。特定の並列弦に対して出力をどういうゲインで与えるかを表す結合係数行列Cを考える。この行列は式(16)のように書くことができる。

ここでNは2偏向弦の組数で、係数gck(K=1,2,3,..,N)はk番めの水平偏向弦からその垂直偏向弦への出力係数。cmkは、k番めの水平偏向弦から、m番めの垂直偏向弦への出力係数である。 行列Cの各要素は、1以下の実数を用いる物理的理由がある。しかし、このシステムはフィードバックがないので、行列の係数には無関係に常に安定である。
Fig11に示したモデルでは、0〜1の値を持つミキシングmpによって、励振信号を垂直弦、水平弦に2分割している。gckを非ゼロにすることで、2つの偏向の間の結合を張ることができる。同時にmpが1であれば、垂直偏向弦はFig11の上の弦のみから結合入力を受ける共鳴弦として働く(注:撥弦による励振がなく結合のみが入力となる)。 結合の例をFig12に示す。
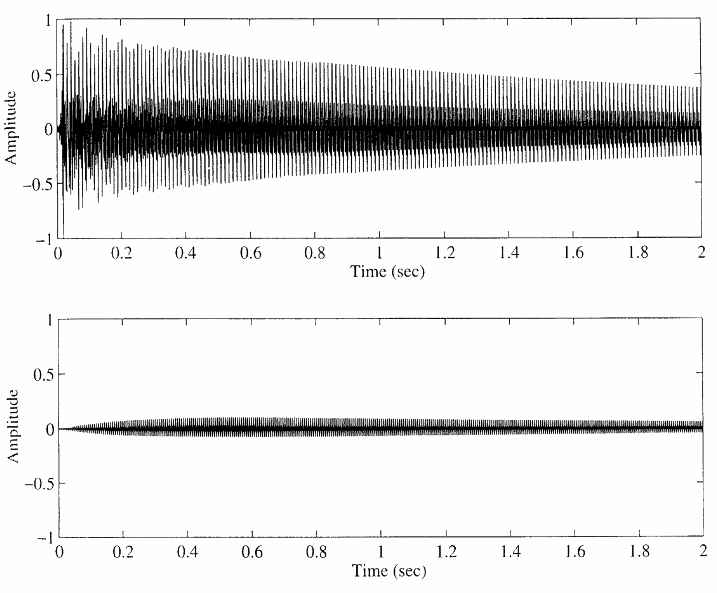
主振動(Fig12の上図に示した)は、図の下に示した副振動からの結合を受ける。この例では、副振動の基本周波数は主振動の1オクターブ上とした。副振動には遅いアタックがかけられている(Fig12下図)。
【さらなる拡張と今後の方向】
撥弦による物理モデル音源研究の将来の方向のトピックスとしては、撥弦のシミュレーション、他の非線型性の導入、弦と胴の間の相互作用、ディジタルフィルタを用いた胴の応答のモデル化、モデルパラメータの校正等がある。これらのうちいくつかは最近の論文で扱っている。RankとKubin(1997)は、弦がフレットと接触することで振動の振幅が制限されるような(スラップベース奏法で用いられるような)非線型モデルを提案している。PierceとVan Duyne(1997)は非線形の受動的なフィルタ構造を開発した。彼らは、弦振動で非線形振動によって、(もとの振動では)欠けている高調波が発生されることを、シ ンプルなディジタルモデルによりうまくシミュレートした例を提示した。胴の応答特性をディジタルフィルタで近似することはKarjalainennとSmith(1996)により議論されている。効率的な計算モデルのためには、胴のモデルを使うことを避け、それをウェーブガイドモデルに含める方が有利である。しかし、弦と胴の双方向の相互作用をシミュレートしようと思ったら、線形時不変系では必要のなかった、胴の明示的なモデルをつくることが可能である。
撥弦モデルのパラメータ値のキャリブレーションはValimakiらによって行われている(1996).提案された方法は、録音された弦の音を短時間フーリエ分析をすることを基本とする。励振信号は録音された音を、弦モデルの逆伝達関数を用いた逆フィルタに通して生成する。これによって、高調波をほぼ指数関数的に減衰させ、高品質の合成をすることができる。この場合問題になるのは、高調波にうなりが生じる場合や、高調波の減衰率が刻々と変化し指数関数以外の変化となるような場合である。この問題に関して、励振信号を、分析する音源の高調波から正弦波を引き算する方法が最近研究されている(Tolonen, Valimaki 1997,Valimaki,Tolonen 1997,Tolonen 1998)。この方法では、高調波の減衰速度の時間的変化を説明し、クリーンな励振信号を提案している。パラメータのキャリブレーションで残された問題は、録音された音から撥弦位置を高い信頼性で推定することである(Valimaki他 1996)。励振信号から、撥弦位置の情報を除去し、撥弦位置による影響をキャンセルすることは有効である。そうした後に、撥弦位置は合成系の自由なパラメータとすることができる。
その他の種類の効果を考慮することで、撥弦音合成音はよりリアルにすることができる。たとえば演奏者が指を弦に沿ってスライドしたり(フリクションノイズ)、ギターの胴を触ったり(Janosy,Karjalainen,Valimaki 1994)というものである。このような効果は、適当なルールで、実時間でトリガされたサンプルを用いたり、これら効果のための物理モデルを改善し表現力と多様性を拡張することで実現できる。さらに、仮想的な撥弦楽器は演奏者が、フレットタッピングのような右手テクニックはもちろん、プルオフ、ハンマーオン、トリル、スラーやスライドの利用のような左手テクニックなど、あらゆる演奏スタイルを取ることを可能にする。JaffeとSmith(1983)はこのようなスタイルのシミュレーションを議論している。それにもかかわらず、これらの演奏技術の、リアルで計算効率が高いモデリングを行うことは未来に残された課題である。
【結論】
本論文では撥弦音の合成に焦点を当てた。撥弦楽器の双方向ディレイラインを持ったディジタルウェーブガイドモデルと、シングルディレイループ(SDL)モデルの関係と、SDLモデルを双方向ディレイラインモデルと等価にする問題を議論した。ディジタルウェーブガイドのアプローチに基づくSDLモデルを、ブリッジ出力とピックアップ出力について導出した。SDLモデルのさらなる拡張として、(弦の間の)結合振動のシミュレーションの新しい方法を含む、いくつかの付加的な特徴をもたせ音質を向上する方法を提案した。
【謝辞】
本論文は筆頭者が1994-1995年にスタンフォード大のCCRMAに滞在中に書いたものが基となっている。Julius O.Smith教授とその学生達と有益な議論ができたことに感謝する
Computer Music Journal Vol22,No.3より引用
物理モデル